Microtonalidad Al Vuelo
Microtonalidad Al Vuelo
- Microtonalidad Al Vuelo
- Preguntas iniciales
- ¿Qué es la microtonalidad? (opinión)
- Algunas preconcepciones en torno a la música microtonal
- ¿Por qué la microtonalidad y la música algorítmica?
- Conceptos fundamentales
- Temperamentos Iguales
- Erv Wilson
- Momento de Simetría (MOS)
- Conjuntos de Combinación de Productos (CPS)
- Ejemplos
- Fuentes
Preguntas iniciales
- ¿Quién está familiarizado con la microtonalidad o con usar recursos armónicos diferentes de la escala de 12 tonos iguales?
- ¿Quien sabe como construir una escala a partir de intervalos?
- ¿Reconocen esto
2 2 1 2 2 2 1?
- ¿Reconocen esto
- ¿Qué saben de la serie de armónicos?
¿Qué es la microtonalidad? (opinión)
- Una serie de técnicas que permiten crear una armonía propia
- Hay teoría por un lado, sí, pero no necesariamente debe tener algo que ver con la prática
- Terreno muy poco explorado, por lo que es fácil encontrar cosas interesantes, que además reflejan nuestra personalidad e intereses (no hay demasiados modelos).
- Ainación != Escala
Algunas preconcepciones en torno a la música microtonal
- Es disonante
- Disonancia cognitiva
- Uso en la música académica
- Es muy teórica y matemática
Al contrario
- La mayor parte de la música del mundo se afina maneras divergentes a la afinación predominante en occidente (12 tonos iguales).
- Muchas veces resulta más consonante (acústicamente) que la resultante con la escala 12 tonos iguales.
- Sí es muy teórica, pero a la hora de tocar, el oído y la preferencias pueden ser suficientes.
¿Por qué la microtonalidad y la música algorítmica?
- Creación de instumentos que respondan a las necesidades de cualquier afinación
- Los algorítmos permiten navegar fácilmente escalas de cualquier dimensión
- Seleccionar sub-escalas o acordes
- Generar melodías
- Explorar las propiedades de una escala
- Seleccionar sub-escalas o acordes
- El código al vuelo es aun más útil porque permite experimentar directamente, sin la interfaz de un DAW e incluso sin la "interfaz" o intermediación de una teoría. Sólo tocamos, exploramos y trabajamos a partir de lo que nos gusta.
Conceptos fundamentales
Serie Armónica
- La mayoría de los sonidos donde percibimos un tono, son sonidos compuestos por frecuencias que siguen la serie armónica
- 1 - Nota Fundamental
- 2 - Octava
- 3 - Quinta Justa + Octava
- 4 - Doble Octava
- 5 - Tercera Mayor + Doble Octava
- 6 - Quinta Justa + Doble Octava
- 7 - Séptima Armónica (o Justa) + Doble Octava
- 8 - Triple Octava
Números Primos
* "Identidades nuevas", i.e. 1, 3, 5, 7
* Los números compuestos son nuevas series armónicas
* 2 es la octava de 1, 6 es la octava de 3, 9 es la quinta de 3
(comment
(ref-rain
:id :ejemplo/serie-armonica-1
:durs [1/2]
:tempo 180
:on-event (on-event
(let [serie (range 1 17)] ;; armonicos 1 - 16
(syn/soft-saw :freq (* 100 (at-index serie)) ;; frecuencia base * # de armónico
:dcy 2))))
(stop)
(ref-rain
:id :ejemplo/serie-armonica-2-melodia
:durs [8]
:tempo 60
:on-event (on-event
(let [armonico 8
serie (range armonico (inc (* 4 armonico)))]
(syn/soft-saw :freq (/ (* 800 (rand-nth serie)) ;; se puede cambiar at-index por rand-nth, para generar melodías
armonico)
:amp 0.7
:atk 1
:dcy (max 2 dur)))))
(stop)
(ref-rain
:id :ejemplo/serie-armonica-3-acordes
:durs [5 5 5 6]
:tempo 60
:on-event (on-event
(let [armonico 8
serie (range armonico (inc (* 2 armonico)))]
(doall (for [n [0 3 5]] ;; acorde: grados 0 3 5 a partir de grado de la escala
(syn/soft-saw :freq (/ (* 200
(wrap-at (+ (at-index [0 1 3 2]) ;; grado de la escala
n) ;; nota del acorde
serie)
(rand-nth [1 2 1/2 4]) ;; seleccionar octava de cada nota al azar
)
armonico)
:amp 0.2
:atk 4
:dcy 4))))))
(stop))
Afinación Justa (Just Intonation, JI)
- Escalas formadas por intervalos que utilizan la serie armónica
- Los intervalos tienen tamaños variables
Temperamento Igual (Equal Temperament or ET; Equal Division or EDO, ED2, ED3...)
- Escalas formas a partir de la división de otro intervalo (usualmente la octava) en partes iguales.
- Los temperamentos con frecuencia se usan aproximar varios intervalos justos.
Unidades de Medida
Cuantifican la distancia entre intervalos.
Cents
* 1200 cents es igual a una octava justa, o la proporción 2:1.
Razones (fracciones)
* Usualmente se usa en conjunto con las escalas de afinación justa
* También ayudan comprender qué intervalos de las escalas de temperamento igual aproximan qué intervalos justos.
Construcción de escalas y acordes dentro de temperamentos iguals
Escala diatónica/mayor (en el 12ET)
tono tono semitono tono tono tono semitono
2 2 1 2 2 2 1 (notar que suma 12)
Acordes
(2 2)(1 2)(2 2 1)
4 3 5 - Acrode mayor
(2 1)(2 2)(1 2 2)
3 4 5 - Acrode menor
Temperamentos Iguales
(require '[erv.edo.core :as edo])
(edo/from-pattern (repeat 1 12)) ;; 12edo
(edo/from-pattern (repeat 1 31)) ;; edo
19, 22, 31 https://en.xen.wiki/w/Table_of_31edo_intervals
Erv Wilson
Teórico mexico-norteamerico descubridor de muchas técnicas las para la creación de afinaciones y escalas. Sus teorías hayan expresión principalmente a través de elegantes representaciones gráficas y geométricas.

Momento de Simetría (MOS)
Escalas cuya estructura es tan simétrica como es posible, sin llegar a ser completamente simética.
Por ejemplo 2 2 1 2 2 2 1 es un MOS, mientras que 2 1 2 1 2 1 2 1 no lo es, por ser perfectamente simética.
Los MOS siempre tienen dos intervalos uno grande y un pequeño. La notación de la escala de arriba puede ser: 5L2s.
Un MOS se genera a partir de un periodo (el número de grados de una escala) y un generador (intervalo que se repite sucesivamente mediante una operación de módulo hasta generar escalas que cumplan con las condiciones de un MOS). Los MOS deben cumplir dos concidiones:
- Constar de dos y sólo dos tamaños distintos de intervalos.
- Que el periodo y el generados sean números co-primos (que no contengan factores comunes).
- Que los intervalos producidos también sean co-primos.
- Que la distribución de estos intervalos sea los igual posible (asegurando la simetría, aunque esto más bien el resultado de proceso).
Por ejemplo, para la escala de 12 tonos, con un generador de un intervalo de tamaño 5 (cuarta justa):

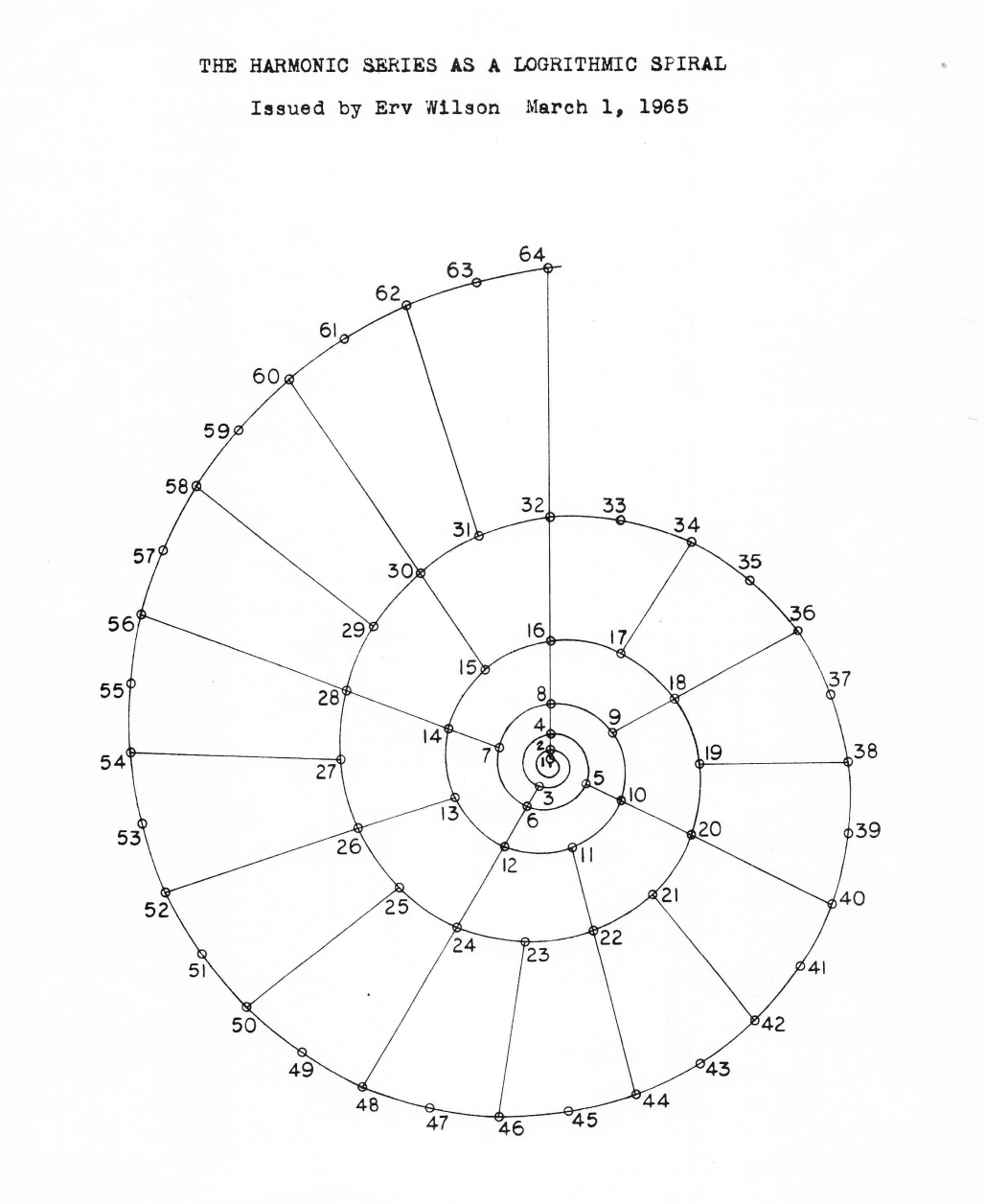
Un MOS también puede ser generado a partir intervalos "irracionales", y pueden ser representados con un círculos. A este modo de representación se le llama un Horograma.
cf. Artículo "Golden Horograms"
También pueden ser usados para generar rítmos: http://www.anaphoria.com/horo2.pdf.
(comment
(let [scale (:scale (edo/from-pattern
;; Escala diatonica 5L2s
#_[2 2 1 2 2 2 1] ;; 12edo
#_[5 5 3 5 5 5 3] ;; 31edo
#_[4 4 1 4 4 4 1] ;; 22edo
;; Antidiatonica 2L5s
#_[2 2 6 2 2 2 6] ;; 22edo
#_[2 2 3 2 2 2 3] ;;16edo
;; OTROS Temperamentos
;; miracle[7] 3L4s
[5 4 5 4 5 4 4] ;; 31 edo
#_[5 3 5 3 5 3 3] ;; 27 edo
#_[6 1 6 1 6 1 1] ;; 22 edo
;; procupine[7] 1L6s
#_[3 3 3 3 3 3 4] ;; 22edo
#_[3 3 3 3 3 3 7] ;; 25edo
#_[4 4 4 4 4 4 7] ;; 31edo
))]
(ref-rain
:id :ejemplo/mos-1
:durs (repeat (inc (count scale)) 1)
:tempo 280
:ratio 1
;; :loop? false
:on-event (on-event
(let [chord (xrepeat [4]
[[0 3 5 7]
[-1 2 5 6]
[-2 2 4 6]
[-3 3 5 6]
[-4 2 5 7]])]
(syn/soft-saw
:freq (scale/deg->freq scale 200 #_(mod index 8)
(at-index chord))
:amp 0.2
:atk 0.1
:dcy 1)))))
(stop))
Rítmos Eucludianos
Todos los rítmos euclidianos son parte de un MOS, pero no todos los MOS son un rítmo euclidiano. Esto significa que los MOS son bastante útiles para el rítmo.
Escalas de 31:
5 5 3 5 5 5 3 - 5L2s. Más cosonante que la escala diatónica de 12ET.
...
Conjuntos de Combinación de Productos (CPS)
Escalas de afinación justa (usualmente) creadas a partir de la combinación y multiplicación de un conjunto de factores.
Si tenemos los factores 1, 3, 5, 7 podemos generar las siguientes combinaciones {1, 3}, {1, 5}, {1, 7}, {3, 5}, {3, 7}, {5, 7}. Por lo que la escala resultante sería:
3 (1*3), 5 (1*5), 7 (1*7), 15 (3*5), 21 (3*7), 35 (5*7)
Si la ponemos dentro de una octava:
35/32, 5/4, 21/16, 3/2, 7/4, 15/8
Notar que no existe el 1 (la fundamental).
Podríamos sin embargo, dividir todos los intervalos por alguno de las notas no octavadas, por ejemplo 35.
1, 8/7, 6/5, 48/35, 8/5, 12/7
Conexiones en los CPS
A la escala de arriba podemos asociarle los factores que constituyen cada nota:
(require '[erv.cps.core :as cps])
(->> (cps/make 2 [1 3 5 7]) ;; combinar tomando 2 de 4 factores
:scale ;; tomar la escala
(map (juxt :bounded-ratio :set))) ;; tomar la proporción interválica octavada (:bounded-ratio) y el conjunto de factores (:set) que le corresponde
;; resultado
[[35/32 #{7 5}]
[5/4 #{1 5}]
[21/16 #{7 3}]
[3/2 #{1 3}]
[7/4 #{7 1}]
[15/8 #{3 5}]]
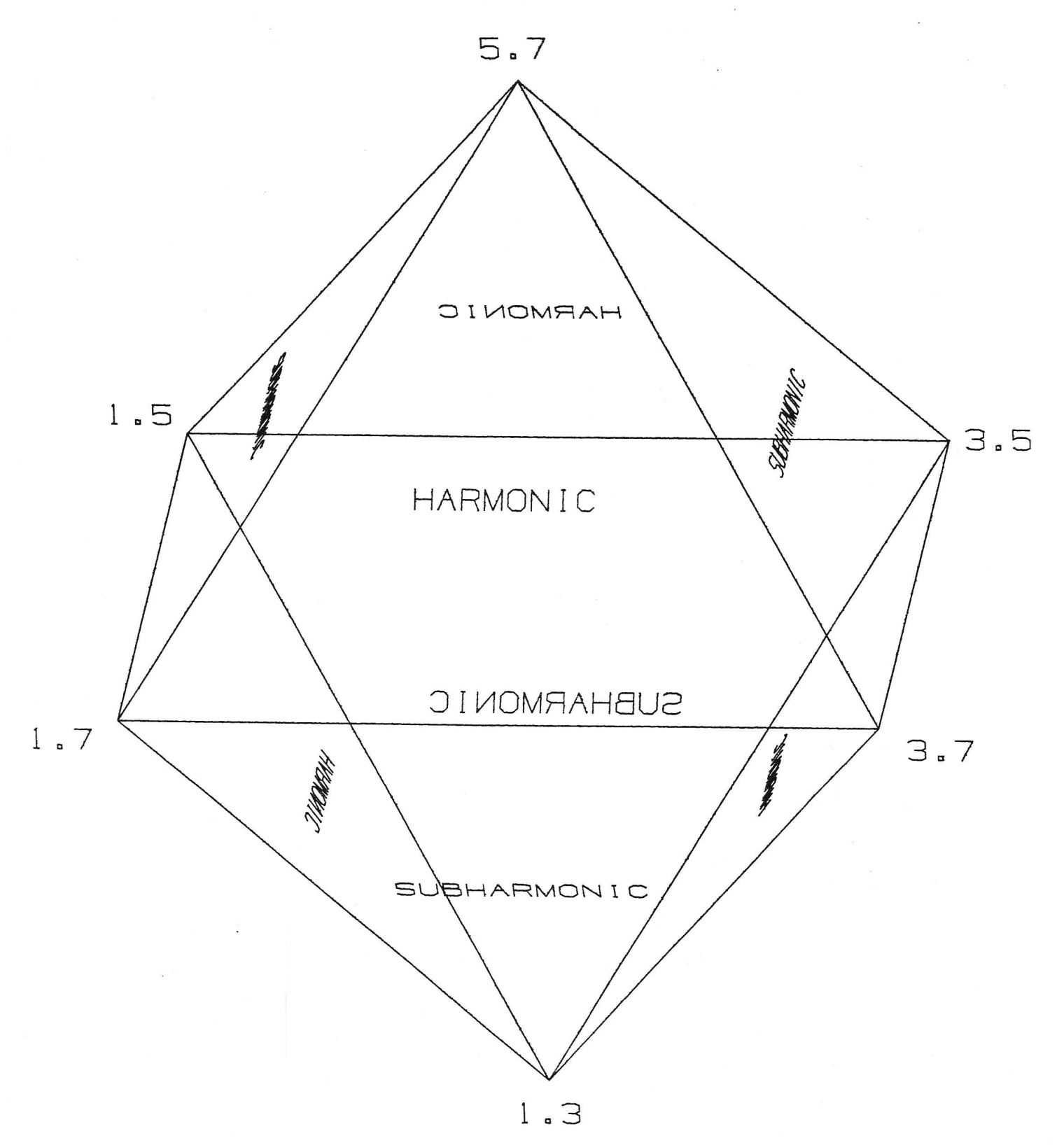
En un CPS, las notas tiene conexiones particularmente interesantes. Tomando la escala de arriba: las notas 7/4 {1 7}, 35/32 {5 7}, 21/16 {3 7} tienen en común el factor 7, por lo que podemos eliminaro de nuestra consideración (y volvera poner las notas resultantes dentro de una octava - es decir entre 1 y 2): (7/4)/7 = 1, (35/32)/7 = 5/4 (21/16)/7 = 3/2,
Los intervalos entre las notas serían 1 - 5/4 - 3/2 es decir, los correspondientes a un acorde mayor tal como lo conocemos.
Por lo que si tocaramos estas tres notas como un acorde o como una melodía tendremos los siguientes intervalos entre estas notas:
Por lo tanto ir de una nota a otra, cuando tienen factores compartidos resulta en intervalos más simples (generalmente más consonantes), que moverse entre notas sin factores compartidos:
7/4 ({1 7}) -> 35/16 ({5 7}) - intervalo: 5/4 (factores involucrados `1 y 5`, dividir entre 1)
vs
7/4 ({1 7}) -> 15/8 ({3 5}) - intervalo: 15/14 (factores involucrados `3, 5, 1 y 7`)
Ejemplo 1
(comment
(let [hexany (cps/make 2 [1 3 5 7])
scale (:scale hexany)
last-note (atom (rand-nth scale))
graph (-> hexany :graphs :full)
get-next-note (fn [last-note]
(-> graph
(get last-note) vec
rand-nth))]
(ref-rain
:id :ejemplo/cps-1
:durs [1]
:tempo 60
:ratio 1
;; :loop? false
:on-event (on-event
(case (mod index 5)
0
((rand-nth [syn/sharp-plate syn/low])
:freq (* 400
(at-index (xrepeat [5 3 1] [4 2 3 1]))
(:bounded-ratio (swap! last-note get-next-note)))
:amp (at-index [0.15 0.1 0.16 0.15 0.06])
:atk (rrand 2.0 4)
:dcy (rrand 5.0 7)
;; :mod-amp (+ 0.1 (* (rand-int 120) 140))
:mod-freq (* (rand-nth (map :ratio scale)) 400))
nil)
(syn/short-plate
:freq (scale/deg->freq scale 200
(+ (at-index [15 13 17 18 9 11]) ;; arpegio
(at-index (xrepeat [16 15 14 13 12 11]
;; transposiciones
[0 1 0 1 2 0 3 1 4 1 5]))))
:amp 0.1
:atk 4
:dcy 1
:mod-amp (+ 0.1 (* (rand-int 120) 140))
:mod-freq (* (rand-nth (map :ratio scale)) 400))))))
Anidamiento y el triángulo de pascal
Una de las características más interesantes de los CPS es que la estructura de sus combinaciones se corresponde con la estructura del triángulo de Pascal.
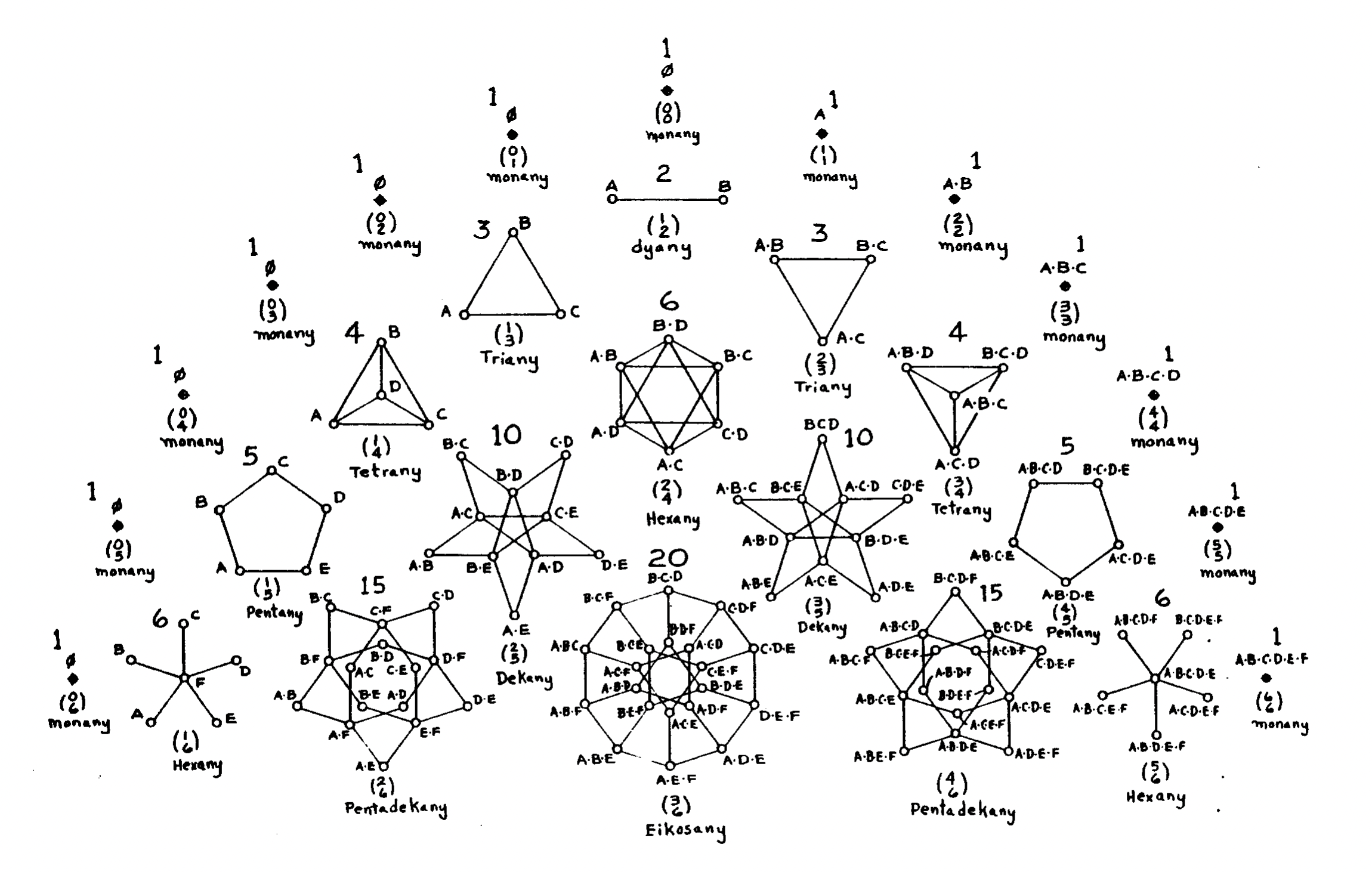
Al mismo tiempo, cada CPS de filas posteriores del triángulo de pascal contiene algunos CPSs de las filas anteriores. Para determinar qué CPSs contienen a qué otros, se puede tranzar un triángulo de Pascal en sentido inverso, partiendo del CPS que uno desea conocer.
Por ejemplo el CPS 2)6 o Hexania, contiene a los siguientes CPSs:
(require '[erv.cps.core :as cps])
(->> (cps/make 2 [1 3 5 7])
(+all-subcps) ;; agregar subconjuntos
:subcps ;; ver los subconjunto
(sort-by first) ;; ordenarlos por nombre
reverse ;; de mayor a menor
(map (juxt first (comp :cps/factors :meta second)))) ;; emparejar nombres con los factores que los constituyen
;; resultado
[["2)3 of 2)4 3.5.7" (3 5 7)]
["2)3 of 2)4 1.5.7" (1 5 7)]
["2)3 of 2)4 1.3.7" (1 3 7)]
["2)3 of 2)4 1.3.5" (1 3 5)]
["2)2 of 2)4 5.7" (5 7)]
["2)2 of 2)4 3.7" (3 7)]
["2)2 of 2)4 3.5" (3 5)]
["2)2 of 2)4 1.7" (1 7)]
["2)2 of 2)4 1.5" (1 5)]
["2)2 of 2)4 1.3" (1 3)]
["1)3 of 2)4 7-1.3.5" (1 3 5 7)]
["1)3 of 2)4 5-1.3.7" (1 3 5 7)]
["1)3 of 2)4 3-1.5.7" (1 3 5 7)]
["1)3 of 2)4 1-3.5.7" (1 3 5 7)]
["1)2 of 2)4 7-3.5" (3 5 7)]
["1)2 of 2)4 7-1.5" (1 5 7)]
["1)2 of 2)4 7-1.3" (1 3 7)]
["1)2 of 2)4 5-3.7" (3 5 7)]
["1)2 of 2)4 5-1.7" (1 5 7)]
["1)2 of 2)4 5-1.3" (1 3 5)]
["1)2 of 2)4 3-5.7" (3 5 7)]
["1)2 of 2)4 3-1.7" (1 3 7)]
["1)2 of 2)4 3-1.5" (1 3 5)]
["1)2 of 2)4 1-5.7" (1 5 7)]
["1)2 of 2)4 1-3.7" (1 3 7)]
["1)2 of 2)4 1-3.5" (1 3 5)]
["1)1 of 2)4 5.7" (5 7)]
["1)1 of 2)4 3.7" (3 7)]
["1)1 of 2)4 3.5" (3 5)]
["1)1 of 2)4 1.7" (1 7)]
["1)1 of 2)4 1.5" (1 5)]
["1)1 of 2)4 1.3" (1 3)]]
Notación
Puesto que los CPS son combinaciones de factores se dice que una CPS combina un X número de elementos a partir de un conjunto Y de factores. Es decir, la notación se escribe formalmente X)Y: se toman _X_ de _Y_.
Por ejemplo CPS que veiamos anteriormente combina dos factores a partir del conjunto 1,3,5,7 de factores, por lo tanto se escribe 2)4.
3 (1*3), 5 (1*5), 7 (1*7), 15 (3*5), 21 (3*7), 35 (5*7)
En mi librería los nombres de los CPS se escriben de la siguiente manera: 2)4 1.3.5.7. El CPS que combina elementos tomando 2 de 4.
En los subconjuntos que se muestran arriba, hay factores que son comunes a todas las combinaciones, por en ese caso se usa un guión para separar a los factores comunes a todas, de los que no lo son, por ejemplo: 1)3 of 2)4 5-1.3.7. Éste nombre se leería de la siguiente manera, el conjunt que toma las combinaciones de un elemento del un conjunto de tres a partir del conjunto de elementos 1,3,7 que tienen todos en común (o están multiplicados por) el factor 5; en realidad, pues, el conjunto de elementos es 1*5, 3*5, 7*5). Por lo que los conjuntos resultantes son:
5 (1*5), 15 (3*5), 35 (5*7)
Que es clarament un subconjunto de 2)4 1.3.5.7
Ejemplos
Sevish (techno/ambient/etc. microtonal, multiples EDOs) https://www.youtube.com/watch?v=xVZy9GUeMqY
Zheana Erose (pop experimental, NEJI - near equal just intonation) https://zheaerosemusic.bandcamp.com/track/wxtchcrxft
Kraig Grady (CPS, JI, estudio directamente con Wilson) https://anaphoria.bandcamp.com/album/the-creation-of-the-worlds
Pirarán (CPS, live coding) https://piraran.bandcamp.com/track/parte-i
Fuentes
Artículos de Wilson https://www.anaphoria.com/wilson.html
XenWiki (Wikipedia de Xenharmonía) https://en.xen.wiki/w/Main_Page
Hear Between the Lines (Youtube, teoría microtonal enfocada en 31EDO) https://www.youtube.com/c/HearBetweenTheLines
Zheana Erose (videos de teória de 31EDO) https://www.youtube.com/watch?v=7cv-nuSjbY4 https://www.youtube.com/watch?v=unuVHCZ2snE https://www.youtube.com/watch?v=uH3ahBzDSrs